Cenni di statica delle murature. Il materiale forte a compressione e debole a trazione

Prima di parlare di statica delle murature è bene precisare che al giorno d’oggi la scienza dei materiali è divenuta così sofisticata che si riescono a progettare materiali dalle caratteristiche ottimizzate in base alla funzione che devono svolgere, materiali talmente controllati che il comportamento alla scala macroscopica e spesso deducibile attraverso tecniche matematiche di omogeneizzazione che incorporano alla scala macroscopica il comportamento meccanico visibile alla scala micro e mesoscopica.

In questo panorama la costruzione in muratura appare, agli occhi di un moderno sperimentatore, come inesorabilmente vecchia e priva di interesse, caratterizzata com’è da una patologica inaffidabilità.

Eppure la forza espressiva di una costruzione in muratura, quale un arco, una volta o una cupola, una torre, rimane tuttora insuperata per la sua ancestrale vicinanza emotiva all’esperienza umana, sollecitando nelle società civili sforzi politici ed economici finalizzati alla manutenzione e conservazione di questi patrimoni della collettività; e qui mi riferisco sia agli edifici monumentali o storici che a quelli dell’edilizia rurale o cosiddetta minore.

Occorre qui sottolineare che l’idea piuttosto diffusa, anche tra molti tecnici moderni, che le strutture in muratura siano poco sicure a causa della debolezza intrinseca del materiale, trova scarsissimo riscontro nella realtà. Le strutture murarie sono strutture massive e la loro sicurezza è affidata principalmente alla geometria ed alle proporzioni della costruzione piuttosto che alla resistenza, la quale ultima riveste solitamente un ruolo secondario.

Il materiale che compone un elemento in muratura può essere modellato come unilaterale, anche se l’accettare il modello unilaterale per la muratura richiede una certa dose di pensiero e di astrazione perché In realtà nessun tipo di muratura, per quanto scadente sia la malta o la qualità dei blocchi, è realmente un materiale unilaterale, ossia totalmente incapace di trasmettere trazioni.

Piuttosto la muratura è un materiale composito elasto-fragile, la cui tenacità e coesione sono molto basse in rapporto alle forze in gioco e, comunque, a causa della scarsa e diversa resistenza a trazione delle sue fasi (blocchi e malta) e del modo imprevedibile in cui la malta aderisce ai blocchi, risulta essere una funzione fortemente oscillante e sostanzialmente aleatoria della posizione. Per cui è più sicuro considerare la muratura come totalmente incapace di resistere a trazione.

Le costruzioni in muratura sono in effetti costruite, sin dai tempi più remoti, facendo affidamento essenzialmente sulla sola resistenza a compressione del materiale.

Leggi anche: Interventi di consolidamento e adeguamento sismico degli edifici in muratura

Cenni di statica delle murature. Assenza di scorrimenti e conservazione della forma

Se è quindi prudente e conveniente considerare la muratura come unilaterale (ma anche necessario vista la impossibilità di definire una soglia certa per l’energia di frattura e quindi per la comunque piccola resistenza a trazione del materiale) è peraltro evidente che la muratura è in grado di sostenere forze di compressione (che possono produrre stati di tensione biassiali o uniassiali) conservando la sua forma.

A proposito di statica delle murature, il modello da adottare per la muratura dovrebbe essere quindi tale da consentire ad una parete in muratura di mantenere stabilmente la propria forma anche in presenza di stati di compressione uniassiale.

I più o meno piccoli blocchi che compongono le costruzioni in muratura sono compattati dalle compressioni in una certa forma iniziale. Tale forma può essere mantenuta solo se le pietre non slittano l’una rispetto all’altra. Un muro soggetto a carichi verticali deve avere la capacità di resistere a slittamenti laterali, per attrito o a causa dell’ingranamento (interlocking) dei blocchi.

Lo slittamento tra le pietre è spesso impedito da chiavi e tenoni previsti proprio per questo scopo. In assenza di tali elementi lo scivolamento è impedito dall’attrito che si sviluppa sulle superfici compresse. Data la dimensione piccola, ma non trascurabile dei blocchi, lo slittamento risulta impedito anche nella direzione parallela alle forze di compressione.

L’assenza di slittamento in direzione parallela alle tensioni uniassiali di compressione è dunque legata alla dimensione piccola, ma finita, delle pietre. Esiste evidentemente una taglia minima dei blocchi: un muro a secco verticale può mantenersi in equilibrio ma è impossibile realizzare con la sabbia una struttura simile e che risulti altrettanto stabile.

Anche se in alcuni rari casi, localmente, si possono osservare scorrimenti tra i blocchi, generalmente le strutture murarie sono in grado di mantenere la loro forma piuttosto bene, specialmente in presenza di tensioni di compressione piccole in rapporto alle tensioni di rottura per schiacciamento.

Potrebbe interessarti: Verifiche elementi non strutturali: passo fondamentale per la sicurezza sismica

Cenni di statica delle murature: il Modello semplificato di Heyman

In effetti c’è un modo semplice di avvicinarsi alla descrizione del comportamento delle costruzioni in muratura, che consiste nell’adottare il modello di Heyman, definito dalle seguenti restrizioni materiali:

1. comportamento unilaterale: il materiale non in grado di trasmettere sforzi di trazione;
2. le fratture, che sono delle soluzioni di continuità di puro distacco che possono verificarsi all’interno dei materiali, si manifestano nella muratura senza slittamenti e a costo energetico nullo;
3. il materiale si comporta rigidamente a compressione.

Il modello semplificato sopra descritto è il primo (se non l’unico) strumento che può essere impiegato per una corretta analisi delle strutture in muratura. L’applicazione di tale modello al caso dell’arco in muratura ne è un esempio efficace.

Prendiamo come esempio l’arco. Si tratta di una struttura curva in muratura che può essere realizzata disponendo i blocchi in modi e forme diversi. Sui manuali di fine ’800, quali quelli del Formenti, si legge:

“Le arcate sono strutture curve nelle quali, come nelle volte, i materiali si reggono per effetto del mutuo contrasto che tra loro si sviluppa … la spinta che le arcate esercitano lateralmente, in due versi opposti, sui pilastri e sulle murature, si possono contrastare ed elidere, con tiranti e catene orizzontali di ferro, fermate agli estremi”.

Da questa descrizione appare evidente come i costruttori del passato avessero ben chiaro il modello poi formalizzato da Heyman e basato sul comportamento unilaterale delle murature: le spinte dell’arco sono un effetto evidente della unilateralità del comportamento della muratura: un arco in materiale bilaterale `e infatti pochissimo spingente.

Una soluzione di equilibrio che comporta solo compressioni si può ottenere immaginando che il peso dei singoli conci di pietra sia sostenuto da due forze di compressione che il concio riceve attraverso le superfici di contatto con i blocchi adiacenti. Le rette d’azione di queste forze interne di contatto (sforzi normali) formano un poligono di forze, detto poligono delle pressioni, che è l’esatto rovescio del poligono funicolare di equilibrio di una fune che sostenga in equilibrio le stesse forze (mostrato anch’esso in fig.1-a).

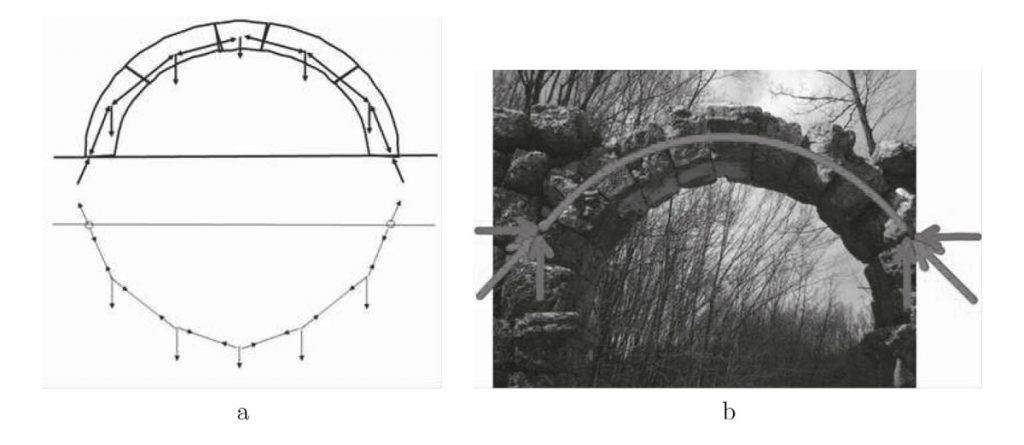
Un arco bimillenario che riproduce esattamente questo tipo di equilibrio è mostrato in fig.1-b. In tale figura il poligono delle forze diviene una curva (linea delle pressioni o linea di spinta), supponendo che il peso del concio non abbia un effetto concentrato ma, piuttosto, di tipo distribuito.

L’articolo (originariamente pubblicato su Ingegneri.cc) è tratto dal volume Statica ed elementi di dinamica  di Maurizio Angelillo, edito da Maggioli Editore.

Acquistalo qui