Momenti di Topografia, dell’incertezza delle misure. Undicesima puntata

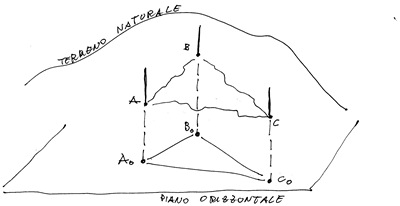
Certo è che le misure riguardano il “modello” assunto per risolvere il particolare problema sotto esame ed è anche certo che tale modello non ha riscontri in natura, se non in maniera ipotetica. Faccio un esempio: quando vogliamo misurare il lati del triangolo ABC, i cui vertici sono segnalati sul terreno da tre paline (vedi figura seguente), in realtà cerchiamo di misurare i lati del triangolo con vertici A₀B₀C₀, proiezioni sul piano orizzontale di quelli sul terreno; in altre parole, andiamo a misurare i lati orizzontali che di fatto non esistono se non come modello di quelli del triangolo “reale”, orizzontalità che viene assicurata solo dallo strumento di misura.

Il modello geometrico, solo pensato, si può dire “perfetto”; quando su di esso si tentano delle misure, come nel caso del triangolo, si entra nel campo dell’esattezza scientifica, in cui è inevitabilmente presente l’errore: le misure sono comunque affette da inesattezze, dovute alla precisione intrinseca dello strumento, all’accuratezza delle operazioni da espletare e alla particolare situazione ambientale in cui si opera.

Se, ad esempio, si fossero misurati i tre angoli piani del “famoso” triangolo, quello proiettato sul piano orizzontale, e se le misure avessero i seguenti valori:

66^o 25’ 33’’; 48^o  18’ 57”; 85^o15’19”,

si riscontrerebbe subito un “errore” in meno di 11″ rispetto ai 180^o dovuti alla somma degli angoli interni di un triangolo piano, come vuole la perfezione geometrica del modello assunto.

Se la somma degli angoli effettivamente misurati sul terreno con la stazione totale desse effettivamente 180^o, due sarebbero i casi:
– il caso ha fatto sì che gli errori su ogni angolo, comunque presenti, si sono compensati in modo tale da rendere la loro somma “perfetta”, la qual cosa appare quasi miracolosa;
– il miracolo non è più dovuto al caso ma alla furbizia del baro.

Siccome non si può essere certi se il caso o la furbizia abbia causato i 180^o, ogniqualvolta si presenta l’eventualità della “perfezione”nelle misurazioni si deve sospettare il peggio, dovendo, a rigore, ripetere le operazioni da capo, con la “speranza” di  percepire l’inevitabile errore: paradossalmente, è quest’ultimo  che rende scientifica l’operazione riducendo i “sospetti”.