Le camice in acciaio, applicate generalmente a pilastri di sezione rettangolare, sono costituite da quattro profili angolari sui quali sono saldate delle piastre in acciaio, nel caso di rinforzo continuo, oppure della bande poste ad un interasse adeguato; in quest’ultimo caso si parla di rinforzo discontinuo. Angolari e calastrelli rappresentano una delle tecniche tradizionali maggiormente utilizzata per l’adeguamento degli elementi esistenti poiché, se ben progettati, si riescono a ottenere moltepliflici effetti sulla struttura.
La molteplice efficiacia è proprio quello che differenzia l’incamiciatura in acciaio dalla maggior parte delle tecniche di rinforzo sismico locale; tra gli effetti si ricordano:
- aumento della capacità di resistenza a taglio;
- aumento della capacità in termini di deformazione;
- aumento di duttilità, attraverso confinamento.
Aumento della resistenza
Come riportato al paragrafo C8.7.4.2.2. della Circolare applicativa alle NTC2018 Il contributo della camicia alla resistenza a taglio può essere considerato aggiuntivo alla resistenza preesistente purché la camicia rimanga interamente in campo elastico. È fondamentale che venga rispettata questa condizione affinchè l’ampiezza delle fessure nel calcestruzzo sia limitata e sia garantito il funzionamento del meccanismo resistente dell’elemento esistente.
La resistenza a taglio aggiuntiva Vj si valuta come:
??=0.5 ???[latex]frac{2???}{?}[/latex]0.9 ?cot?
dove tj, d e s sono rispettivamente lo spessore, la larghezza e il passo delle bande in acciaio (se la camicia è continua b/s =1); d è l’altezza utile della sezione, fyw la tensione di snervamento dell’accaio e θ l’inclinazione delle fessure per taglio. Come si può osservare, la formula limita al 50% la tensione di snervamento dell’accaio.
Allo SLU si ottiene anche un incremento di resistenza a compressione NRd, limitando sempre la resistenza della camicia al 50%.
???=??0+4 ?? 0.5 ???
essendo NR0 la resistenza a compressione della sezione prima del rinforzo e As l’area del singolo angolare.
Effetto del confinamento
L’incamiciatura, ai fini del confinamento, ha lo stesso effetto delle staffe. L’obiettivo che si vuole perseguire è quindi, un aumento della resistenza e della deformazione del calcestruzzo, riuscendo a percorrere un legame tensione-deformazione più ampio (Figura 1).
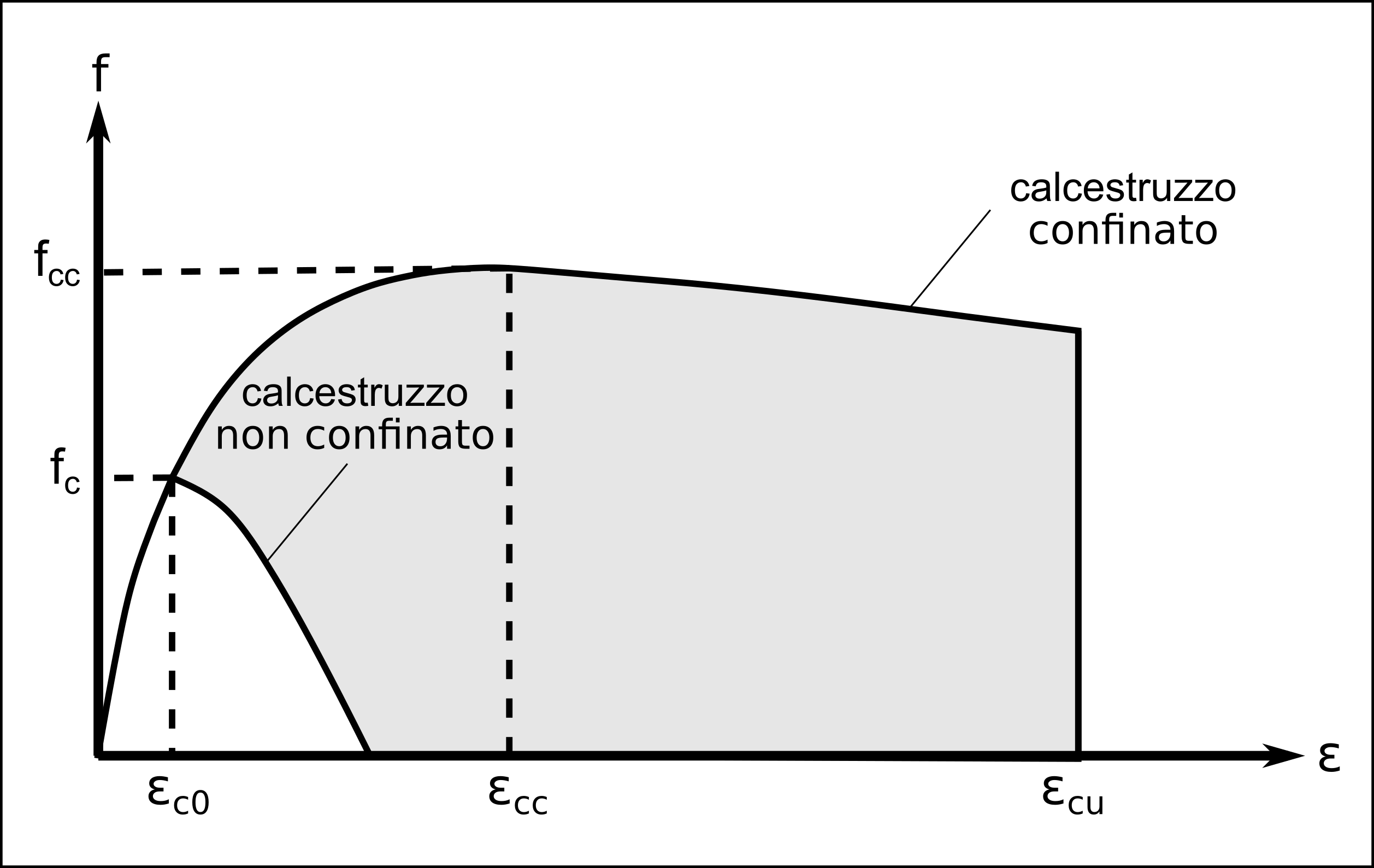
Per la definizione delle resistenze e della duttilità del calcestruzzo confinato è necessario introdurre i seguenti parametri:
- rapporto volumetrico dell’armatura trasversale ρs, pari, nel caso di camicie continue, a:
??= [latex]frac{2 (? +ℎ)}{? ℎ} [/latex]
essendo b e h le dimensioni della sezione in calcestruzzo e ts lo spessore della camicia; nel caso di bande discontinue vale:
??=[latex]frac{2 ??(?+ℎ)}{? ℎ ?} [/latex]
essendo As l’area trasversale della banda e s il passo delle stesse.
- Fattore di efficienza del confinamento nel piano della sezione αn e lungo l’elemento αs:
??=1− [latex]frac{(?−2?)²+(ℎ−2?)²}{3 ? ℎ}[/latex]
??=(1−[latex]frac{?−ℎ?}{2?})[/latex](1− [latex]frac{?−ℎ?}{2ℎ})[/latex]
dove R è il raggio di arrotondamento degli spigoli della sezione: per gli angolari si assume pari al minimo tra la lunghezza del lato e 5 volte lo spessore degli stessi; b e h sono le dimensioni della sezione e hs è l’altezza delle bande discontinue, pari a s nel caso di camicia continua.
Tali coefficienti non sono nient’altro che il rapporto tra l’area di calcestruzzo realmente confinata per la presenza dell’incamiciatura e l’area totale della sezione. È noto, infatti, che l’azione di confinamento non è costante ma perde di efficacia man mano che si ci allontana dagli elementi in acciaio.
Per la corretta interpretazione del coefficiente di efficienza di confinamento orizzontale si faccia riferimento alla seguente figura:
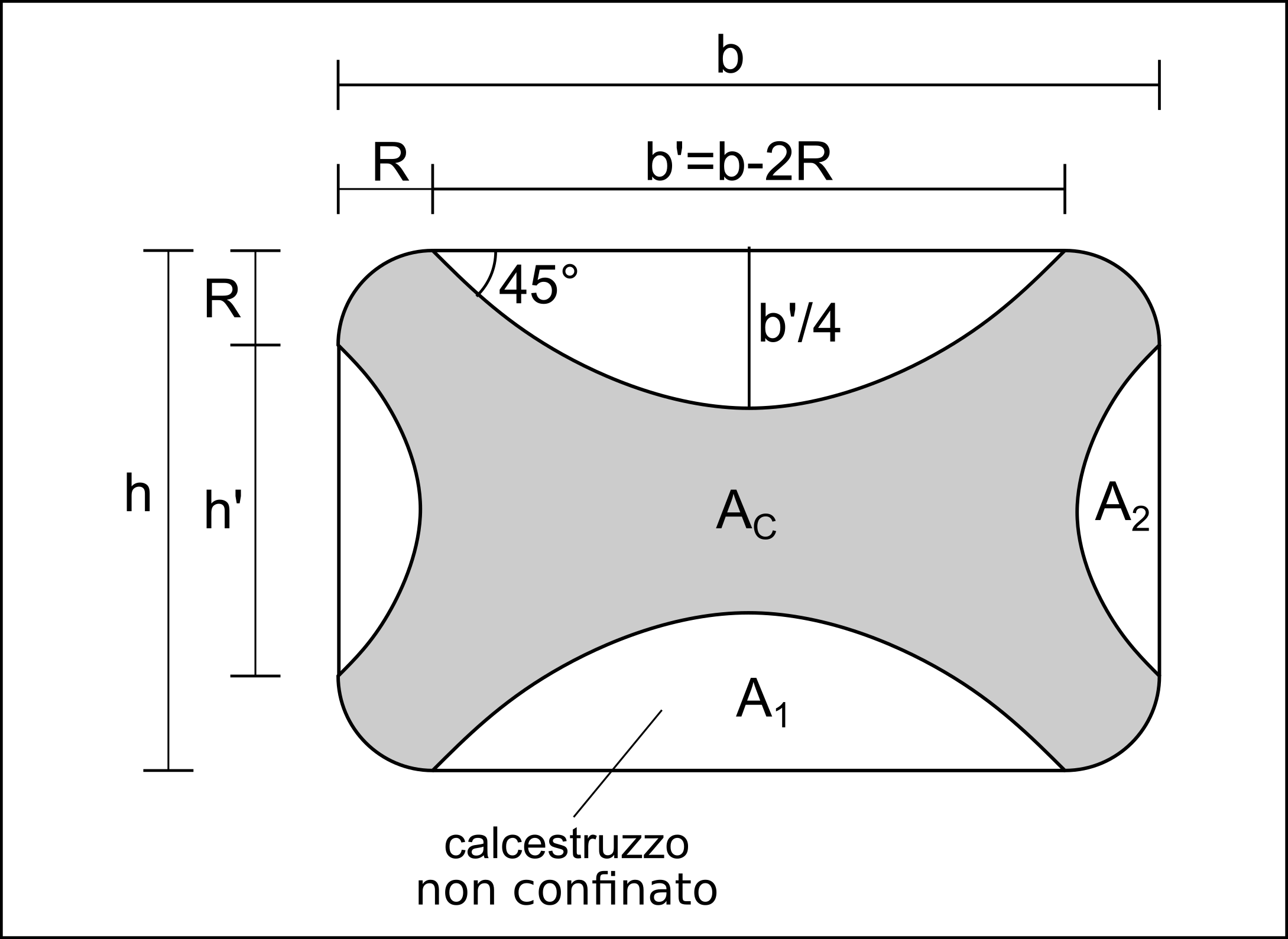
In una sezione rettangolare in calcestruzzo, l’effetto del confinamento è concentrato in corrispondenza degli spigoli degli angolari; la porzione di elemento ben confinata è usualmente individuata da una parabola con pendenza a 45° in corrispondenza dell’elemento in acciaio.
Indicando con b’=b-2R la distanza tra gli angolari, l’altezza di ciascun segmento parabolico è pari a b’/4. Ricordando che l’altezza media di un segmento parabolico è i 2/3 dell’altezza massima, l’area A1 della porzione di sezione non confinata vale:
?1=[latex]frac{2}{3}frac{?′}{4} ?′=frac{1}{6}(?′)²=frac{1}{6}(?−2?)²[/latex]
Analogamente:
?2=[latex]frac{2}{3}frac{ℎ′}{4}?′=frac{1}{6}(ℎ′)²=frac{1}{6}(ℎ−2?)²[/latex]
Pertanto l’area totale della sezione confinata sarà:
??=????−2?1−2?2
=[latex]?ℎ− frac{1}{3}(?−2?)²−frac{1}{3}(ℎ−2?)²[/latex]
=[latex]?ℎ− frac{((?−2?)²+(ℎ−2?)²}{3}[/latex]
di conseguenza:
??=[latex]frac{??}{????}=1−frac{(?−2?)²+(ℎ−2?)²}{3 ? ℎ}[/latex]
In modo del tutto analogo si può ricavare il fattore di efficienza verticale (si faccia riferimento all’immagine successiva).
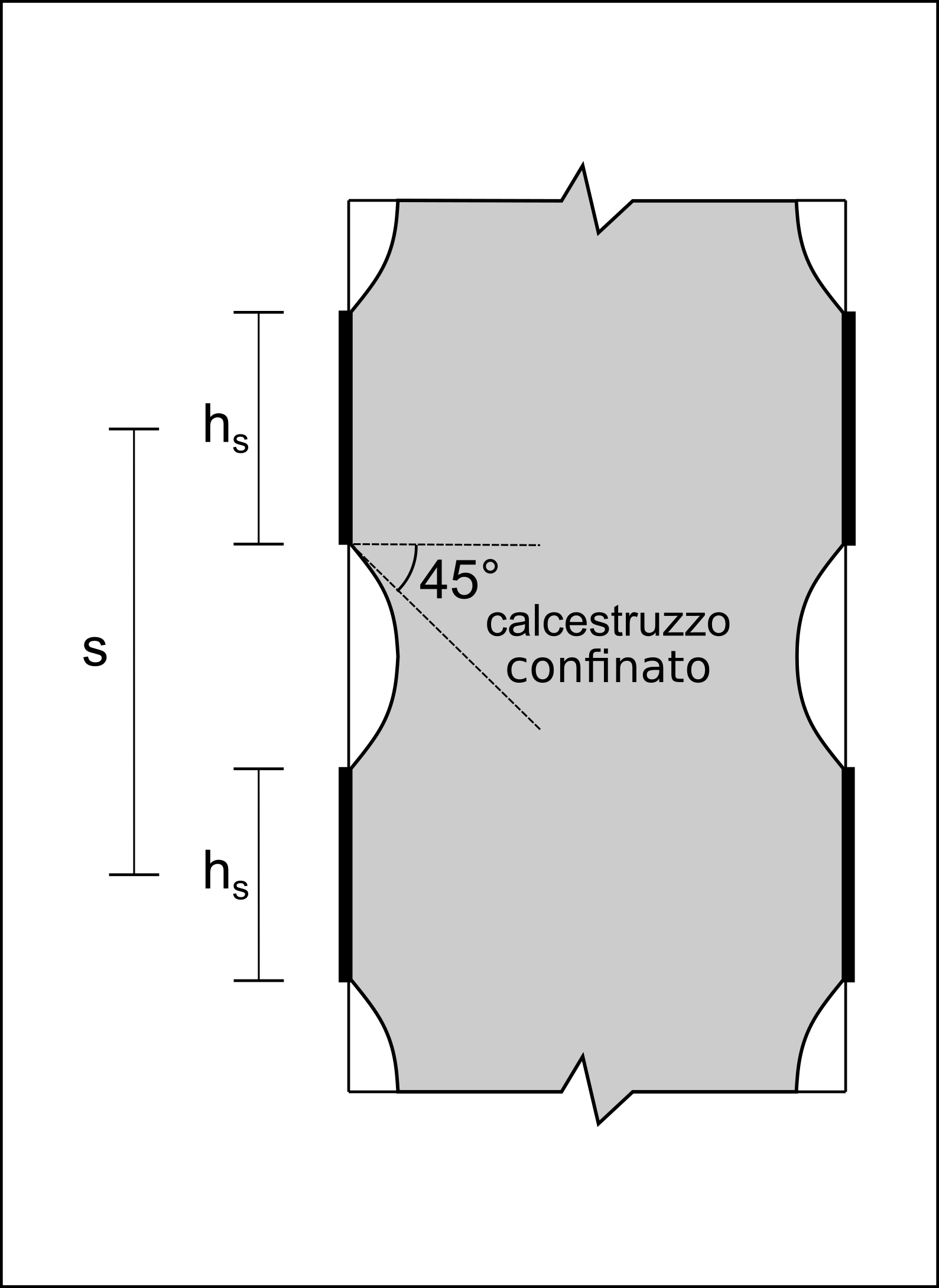
La resistenza del calcestruzzo confinato e la deformazione ultima valgono rispettivamente:
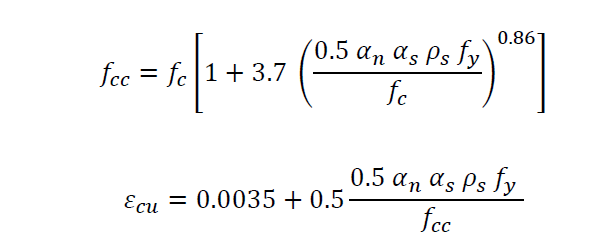
Essendo fc la resistenza del calcestruzzo non confinato e fy la resistenza a snervamento degli elementi di rinforzo. La resistenza del calcestruzzo è quella media derivante da prove in situ, opportunamente divisa per il fattore di confidenza appropriato al Livello di Conoscenza; la resistenza dell’acciaio del rinforzo è quella di calcolo.
L’inserimento degli angolari e calastrelli su una struttura esistente modellata in IperSpaceBIM presuppone che essi siano definiti all’interno delle Tavolozze – Rinforzi. Tutte le caratteristiche meccaniche e geometriche del rinforzo possono essere definite all’interno della finestra delle proprietà ad essi associata.
In Figura 4 sono riportate, a titolo di esempio, le proprietà relative a un rinforzo per pilastri.
>>>>> Ti piacciono articoli come questo? Ricevili direttamente
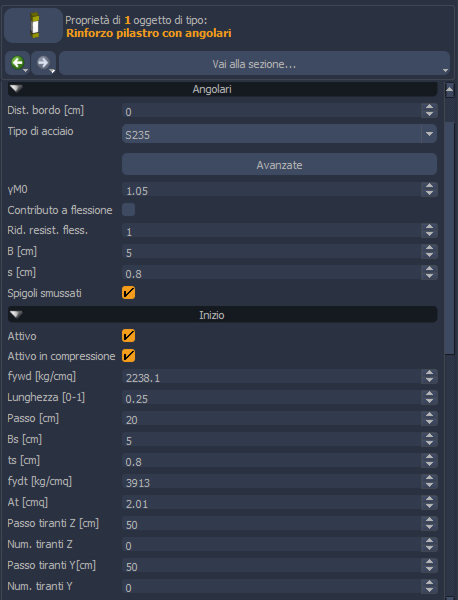
La sottosezione Angolari permette di definire, tra le altre cose, se considerare la presenza del rinforzo anche nella valutazione delle flessione; in particolare è bene prestare attenzione al parametro di Riduzione di resistenza a flessione per ridotta aderenza acciaio – calcestruzzo. Se l’aderenza tra elemento esistente e rinforzo è solo di tipo attritivo tale parametro sarà sicuramente minore dell’unità.
Molte volte, infatti, per facilità di esecuzione si preferisce non tassellare gli angolari alla sezione in c.a., ma effettuare l’accoppiamento attraverso delle malte (a ritiro compensato). Per tale ragione, l’incremento di capacità portante in compressione e flessione associato agli angolari è spesso trascurato; ciò significa che l’incremento di resistenza è attribuito al solo effetto dato dal confinamento.
Alcuni studi, in realtà, hanno dimostrato che, nel caso in cui non siano garantito il contatto tra le estremità, gli elementi in acciaio riescono comunque a fornire un contributo flessionale; contributo che dipende dalla coesione e il coefficiente di attrito all’interfaccia.
Le altre sezioni sono invece relative alle caratteristiche dei calastrelli lungo l’elemento: Inizio, Centro e Fine; è comunque l’utente a scegliere la lunghezza adimensionalizzata di ogni tratto. In questo modo è possibile modellare anche un rinforzo caratterizzato da bande di acciaio non disposte a passo costante lungo la sezione.
Un esempio concreto di verifica della struttura esistente
Si riporta di seguito un esempio realizzato in IperSpaceBIM 4 di una struttura esistente in c.a., realizzata a Benevento (Sottosuolo di tipo C e categoria Topografica T1). Dall’analisi sismica, condotta ipotizzando di aver raggiunto un livello di conoscenza 2 (FC=1.2) è emerso che la maggior parte dei pilastri non fossero verificati né a taglio né a flessione.
Tutti i pilastri, di dimensioni 30 x 50 cm, sono realizzati in calcestruzzo C20/25 e armati con 3φ16 sia superiormente che inferiormente, con l’aggiunta di 1φ16 lateralmente; le staffe sono disposte ad un passo di 30 cm nelle zone iniziali e finali dell’elemento (di lunghezza pari al 10% di quella totale) e ad un passo di 50 cm nella restante zona centrale. L’acciaio utilizzato è il B450C.
In fase di analisi si è utilizzato un valore del fattore di comportamento pari a 2 e 1.5, rispettivamente per le verifiche duttili e fragili.
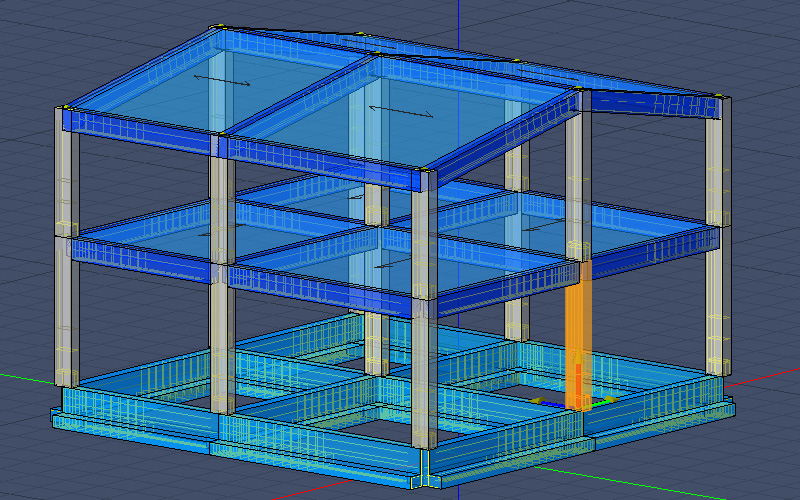
Si è scelto di rinforzare, a titolo di esempio, il pilastro evidenziato in Figura 5.
I risultati dell’analisi sono riportati nella tabelle seguenti, direttamente fornite dal software come output dell’analisi.
Verifica a flessione
| Zona | C. | N | My | Mz | Mry+ | Mrz+ | Mry- | Mrz- | ζE |
| kg | kg*m | kg*m | kg*m | kg*m | kg*m | kg*m | |||
| Piede | (4+5)-I-4(+) | -27198 | 3251 | -15268 | 18439 | 10521 | 18439 | 10521 | 0.66 |
| Testa | (4+5)-I-4(+) | -25885 | -4603 | 15396 | 18238 | 10400 | 18238 | 10400 | 0.63 |
Verifica a taglio
| Dir | C. | MrSup | MrInf | T | VRd,f | Vrdns | Vrcd | Vrsd | Vrd | Ast/m | cot(θ) | ζE |
| kg*m | kg*m | kg | kg | kg | kg | kg | kg | cmq/m | ||||
| Y | (4+5)-I-4 | — | — | 12102 | 0 | — | 24325 | 3983 | 3983 | 2.01 | 2.500 | 0.33 |
| Z | (4+5)-II-4 | — | — | 7313 | 0 | — | 26124 | 6933 | 6933 | 2.01 | 2.500 | 0.94 |
Il pilastro in esame è stato successivamente rinforzato con angolari di larghezza e spessore pari rispettivamente a 5 cm e 0.8 cm. I calastrelli, larghi 5 cm e spessi 0.8 cm, sono stati disposti ad un passo costante tra loro pari a 20 cm; non sono presenti tiranti aggiuntivi. Si è considerato anche il contributo alla resistenza a flessione, ridotto del 50% rispetto a quello totale.
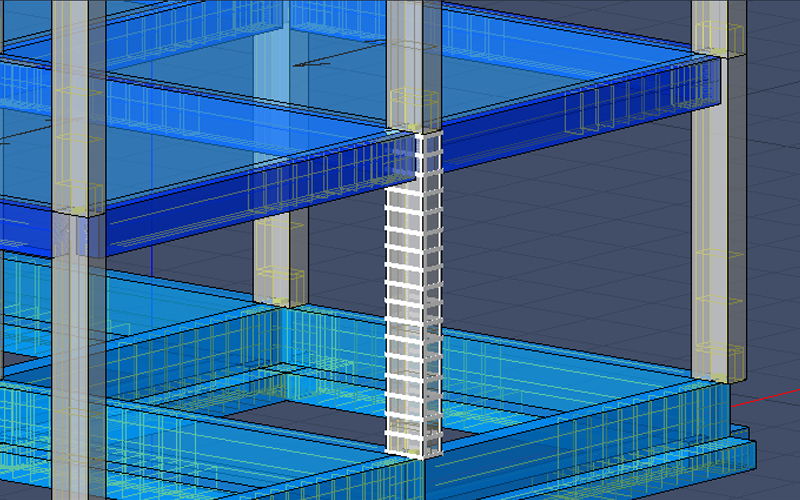
I risultati sono di seguito riportati.
Verifica a flessione
| Zona | C. | N | My | Mz | Mry+ | Mrz+ | Mry- | Mrz- | ζE |
| kg | kg*m | kg*m | kg*m | kg*m | kg*m | kg*m | |||
| Piede | (4+5)-I-4(+) | -27198 | 3251 | -15268 | 19749 | 11252 | 19749 | 11252 | 0.73 |
| Testa | (4+5)-V-4(+) | -25603 | -4718 | 13231 | 18817 | 12974 | 26545 | 12974 | 0.98 |
Verifica a taglio
| Dir | C. | MrSup | MrInf | T | VRd,f | Vrdns | Vrcd | Vrsd | Vrd | Ast/m | cot(θ) | ζE |
| kg*m | kg*m | kg | kg | kg | kg | kg | kg | cmq/m | ||||
| Y | (4+5)-I-4 | — | — | 12102 | 23472 | — | 26910 | 3438 | 26910 | 2.01 | 2.158 | 2.2 |
| Z | (4+5)-II-4 | — | — | 7313 | 29878 | — | 34254 | 4376 | 34254 | 2.01 | 1.578 | 5.3 |
Dalle verifiche effettuate si può notare il miglioramento ottenuto, soprattutto in termini di resistenza a taglio. Da ricordare che il software di calcolo strutturale BIM oriented è aggiornato alle NTC 2018 e alla Circolare esplicativa.
Per saperne di più sul calcolo strutturale e la geotecnica:
Soft.Lab
Foto: iStock/AzmanL























Scrivi un commento
Accedi per poter inserire un commento